参数曲线就是在一个方程表达式中，将方程中的各个系数和常数都用参数变量来表示，并绘制出相应的函数曲线。当这些参数变量发生变化时，函数曲线随之变化，从而直观的展现出曲线的动态变化，反映出各参数与函数曲线的关系，加深对各种函数曲线的理解。

例如：二次曲线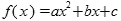，其中：a、b、c是方程的系数和常数。如果a、b、c都是参数变量，那么当a、b、c发生变化时，就可以清楚地观察二次曲线的动态变化。

下面就以“二次曲线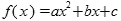”为例，说明参数曲线的应用。

操作：

A.         绘制直角坐标系。

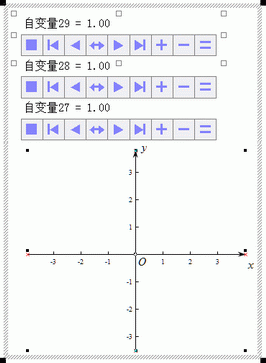
B.        设置参数变量：

a）      设置参数变量a：单击“自变量”图标，出现自变量对话框，设置：“当前值”为1、速度为1、“范围”为-3.14~3.14，确认后得到“自变量27”，即参数a 。

b）      设置参数变量b：按照“设置参数变量a”的方法，获得“自变量28”，即参数b 。

c）      设置参数变量c：按照“设置参数变量a”的方法，获得“自变量29”，即参数c 。

绘制坐标系	定义自变量27、28、29

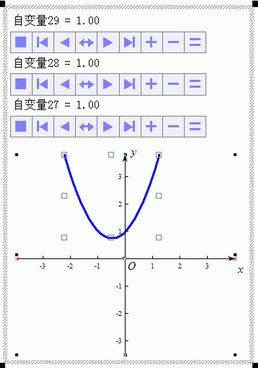
C.        绘制参数曲线：单击“带参数的一般曲线”图标，出现参数曲线对话框，输入：f(x)=a*x^2+b*x+c、参数个数为3、参数a选择“自变量27”、参数b选择“自变量28”、参数c选择“自变量29”，然后确认，获得函数曲线。

说明：

         输入方程的类型可以是对话框右边“函数列表”中任何一个函数方程，“函数列表”说明请参看附录3。

         双击“函数列表”中函数项，可以直接进入“f(x)=”的输入框。

D.        设置函数曲线的属性：单击选中函数曲线，在几何作图工具栏上，单击颜色图标设置曲线颜色为“蓝色”、单击线宽图标设置为0.75。

E.         触发自变量变化按钮，启动参数变化，观察曲线：

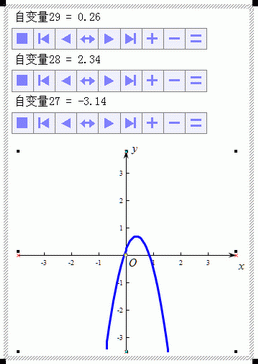
a）      单击“自变量27”下面的变化按钮（减小、双向、增大），可以看到：随着“自变量27”的变化，函数曲线随之变化，直观展现出函数曲线与系数a的关系。

b）      同样，单击“自变量28”或“自变量29”下面的变化按钮（减小、双向、增大），可以观察函数曲线与系数b或常数c的关系。

绘制参数曲线，并设置属性	触发自变量按钮，观察曲线变化

通过上面说明，可以了解并掌握参数曲线的设计思路和操作方式，基于上面的“自变量27”、“自变量28”、“自变量29”和坐标系，将方程设置为另外的曲线方程，可以观察不同函数曲线的变化。

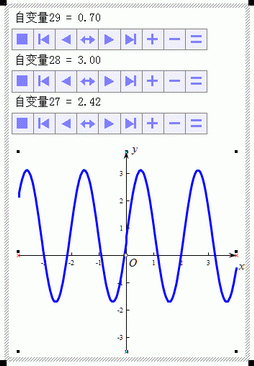
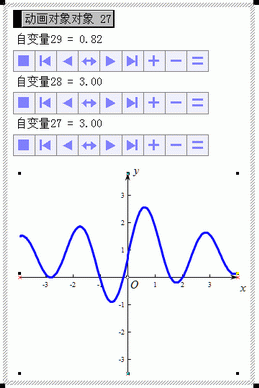
例如：按照上面第3）步，输入方程为：正弦f(x)=a*sin(b*x)+c、n阶贝塞尔函数f(x)=a*jn(1,b*x)+c，可以绘制出正弦曲线、n阶贝塞尔曲线，此时触发自变量变化按钮，可以观察正弦曲线、n阶贝塞尔曲线随参数变化的情况。

正弦曲线随参数变化	n阶贝塞尔曲线随参数变化